数学建模
析没有考虑到90%的到达几率限制,但在设计算法需要充分考虑。
综上所述,当警车静止在初始停靠 时,在三分钟时间限制
时,在三分钟时间限制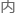 ,警车能从初始停靠
,警车能从初始停靠 赶到事发现场的最大距离为。
赶到事发现场的最大距离为。
5.1.2 将 路离散化
路离散化
由于事发现场是等概率地分布在 路上的,由区域地图可以发现,整个区域中的
路上的,由区域地图可以发现,整个区域中的 路长度不均,为了使计算结果更加
路长度不均,为了使计算结果更加 确,可将这些
确,可将这些 路离散化。只要选取适宜的离散方案,就能使警车在经过
路离散化。只要选取适宜的离散方案,就能使警车在经过 路上的离散的
路上的离散的 时就相当于经过了这条
时就相当于经过了这条 路。这样,不
路。这样,不 是求解警车初始停靠
是求解警车初始停靠 还求解警车赶到事发现场所经过的
还求解警车赶到事发现场所经过的 路时,所计算得的的结果显然比仅考虑整条
路时,所计算得的的结果显然比仅考虑整条 路的叉路
路的叉路 要
要 确得多。
确得多。
区域中共有307个 路交叉
路交叉 ,458条
,458条 路。我们采用线
路。我们采用线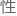
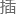 值方法对
值方法对 路
路 行离散化,以的速度行走一分钟的距离作为步长,一分钟时间的选择是参照问题三的结果要求来设定的,步长。用线
行离散化,以的速度行走一分钟的距离作为步长,一分钟时间的选择是参照问题三的结果要求来设定的,步长。用线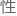
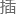 值的方法,从
值的方法,从 路的一个方向
路的一个方向 行线
行线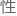
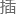 值,实现将每条
值,实现将每条 路离散化的目标,考虑到有些
路离散化的目标,考虑到有些 路不是的整数倍,我们就一般
路不是的整数倍,我们就一般 况
况 行讨论,其分析示意图如图3所示。
行讨论,其分析示意图如图3所示。 路AB长度为个与长度的和,为了更
路AB长度为个与长度的和,为了更 确
确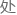 理CB段
理CB段 路,那么就要考虑在CB之间是否要
路,那么就要考虑在CB之间是否要
 一个新的
一个新的 ,
, 据的长度不同,其对应的
据的长度不同,其对应的 理方式也有所不同。
理方式也有所不同。
图3  路离散化分析示意图
路离散化分析示意图
引 临界指数,选取大小的准那么是使尽量离散化后警车等效的平均巡逻速度和题目给定的速度〔〕的差值尽量小,经过计算得时,不再
临界指数,选取大小的准那么是使尽量离散化后警车等效的平均巡逻速度和题目给定的速度〔〕的差值尽量小,经过计算得时,不再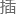
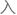 新的坐标
新的坐标 时能使整个区域的
时能使整个区域的 路离散效果较好。此时,将CB段长度设定为
路离散效果较好。此时,将CB段长度设定为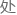 理,于是离散后的AB
理,于是离散后的AB 路长度会比实际长度短些;当时,需要在两个
路长度会比实际长度短些;当时,需要在两个 之间再
之间再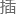
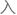 一
一 ,因为这样
,因为这样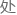 理能使整个区域的整
理能使整个区域的整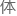
 路的离散化效果比拟理想。如图3所示,在C与B间再
路的离散化效果比拟理想。如图3所示,在C与B间再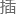
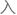 新的坐标
新的坐标 ,
,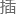
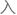 的位置在距C
的位置在距C 的D
的D
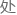 ,这样
,这样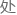 理后所得的
理后所得的 路长度比实际长度长了。采用这样的方法
路长度比实际长度长了。采用这样的方法 行线
行线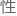
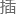 值,我们使用MATLAB编程实现对整个区域
值,我们使用MATLAB编程实现对整个区域 路的离散,所得的离散结果如图4所示,离散后共得到762个节
路的离散,所得的离散结果如图4所示,离散后共得到762个节 ,比原始数据多了455个节
,比原始数据多了455个节 ,离散后的节
,离散后的节 数据见附件中的“newpoint.txt〞。
数据见附件中的“newpoint.txt〞。
图4 整个区域离散结果图
采用这种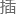 值方法
值方法 路离散后,将直线上的无穷多个
路离散后,将直线上的无穷多个 转化有限个
转化有限个 ,便于分析问题和实现相应的算法,由图4可知,所取得的整
,便于分析问题和实现相应的算法,由图4可知,所取得的整 离散效果还是比拟理想的。
离散效果还是比拟理想的。
5.1.3 分区域求解警车数目的算法设计
考虑到警车 置和巡逻方案需要满足:警车在接警后三分钟
置和巡逻方案需要满足:警车在接警后三分钟 赶到普通
赶到普通 位案发现场的比例不低于90%,赶到重
位案发现场的比例不低于90%,赶到重
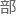 位必须控制在两分钟之
位必须控制在两分钟之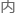 的要求。设计算法的目标就是求解
的要求。设计算法的目标就是求解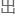 在满足D1
在满足D1 况
况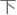 ,总的警车数目最小,即每个区域都尽可能多地覆盖
,总的警车数目最小,即每个区域都尽可能多地覆盖 路节
路节 。由于警车的初始位置是未知的,我们可设警车初始停靠
。由于警车的初始位置是未知的,我们可设警车初始停靠 在
在 路上的任一
路上的任一 ,即分布在图4所示的762个离散
,即分布在图4所示的762个离散 中的某些
中的某些 节
节 上,总
上,总 思路是让每两辆车之间尽量分散地分布,一辆警车
思路是让每两辆车之间尽量分散地分布,一辆警车 辖一个分区,用这些分区覆盖整个区域。
辖一个分区,用这些分区覆盖整个区域。
于是我们设计算法1,步骤如 所示:
所示:
Step1:将整个区域预分 为个分区,每个分区分
为个分区,每个分区分 一辆警车,警车的初始停靠位置设在预分
一辆警车,警车的初始停靠位置设在预分 区中心的
区中心的 路节
路节 上,假设区域的中心不在
上,假设区域的中心不在 路节
路节 上,那么将警车放在离中心最近的
上,那么将警车放在离中心最近的 路节
路节 上;
上;
Step2:统计分区不能覆盖的节 ,调整警车的初始停靠
,调整警车的初始停靠 ,使分区覆盖尽可能多的
,使分区覆盖尽可能多的 路节
路节 ,调整分为区
,调整分为区 调整和区间调整方案:〔1〕区
调整和区间调整方案:〔1〕区 调整
调整 照模拟退火思想构造的函数,在区间调整调整车辆初始
照模拟退火思想构造的函数,在区间调整调整车辆初始 的位置〔后文中有详细说明〕,当分区
的位置〔后文中有详细说明〕,当分区 节
节 数较多时,调整的概率小些,分区
数较多时,调整的概率小些,分区 节
节 数较少时,调整的概率大些,〔2〕当区域中存在未被覆盖的节
数较少时,调整的概率大些,〔2〕当区域中存在未被覆盖的节 或节
或节 群〔大于等于三个节
群〔大于等于三个节 集中在一个范围
集中在一个范围 〕时,将警车初始位置的调整方向为朝着这些未被覆盖的节
〕时,将警车初始位置的调整方向为朝着这些未被覆盖的节
 一定的规那么〔在
一定的规那么〔在