些巡逻盲区。分布很不均衡。这样就可能现巡逻密度大的街上的违法犯罪分不敢在街上作案，而窜到巡逻密度稀疏的街上作案，因此在相同的警车数目条件，密度不均衡的巡逻方式的巡逻效果的效果较差，而密度较均衡的巡逻方式所取得的巡逻效果会更好些。我们引一个巡逻的不均匀度来衡量巡逻效果的显著，考虑到方差能表示不均衡度，于是我们用方差的大小来表征不均衡，方差越大，巡逻密度越不均衡，所取得的巡逻效果越差。

        〔4〕

        问题1所给的满足D1条件的警车数目为13辆，这时每辆警车在初始停靠静止不动，只有该辖区域发生了案件时，警车才从初始停靠赶到案发现场理案件。当警车在巡逻状态时，所需要考虑的问题就更复杂一些，如当节运动时，警车还能否到达D1的要求，警车的运动方向如何等问题，但本算法思想与问题1类似，所得的算法2的框图如图7所示，

        为了简化问题，我们假设各分区警车的巡逻时候，尽量保证所有的警车的行驶方向相一致，且警车都走双行，即当警车走到某个节后，它们又同时返回初始停靠，警车的行驶方向有四种方式，如6所示。

        在图6中，数字1代表走巡逻走的第一步，2表示朝1的巡逻方向相反的方向巡逻。在程序实现时，四种巡逻方向任意选择，但是尽量保证所有的警车向同一个方向巡逻。

        图6            各警车巡逻方向图

        我们用MATLAB编程对这种巡逻方式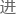行计算，所得的车辆数目为18辆，综合评价指标为，其结果巡逻方案见附件中的“1193402-Result3.txt〞所示。

        在满足问题三的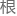底上讨论D3条件，警车的巡逻方案和评价指标

        巡逻的隐蔽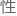表达在警车的巡逻路线和时间没有明显的规律，主要目的是让违法犯罪分无可乘之机，防止他们在非巡逻时间实施违法犯罪活动，危害人民的生命和财产平安。

        为了使巡逻的规律有隐蔽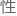，这就需要警车在巡逻时至少有两条不同的路线，时间最好也是不相同的。因此，考虑到隐蔽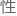时，只需要在问题2的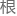底上加上一个随机过程即可。对于其评价指标，由于警车有几条可选的巡逻路线，当相同的路线在同一时间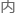重复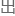现时，重新将所设定的方案再执行一遍，我们用这个时间间隔来衡量隐蔽的程度，当循环周期越大，说明可选的巡逻方案越多，其规律就越有隐蔽，而循环周期越小时，说明巡逻方案比拟少，其隐蔽较差。在巡逻状态时，最差的隐蔽巡逻方案是巡逻方案只有一个，并且时间固定，这样的巡逻方案没有任何隐蔽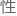可言。

        5.5            整个区域为10辆车时的巡逻方案

        由第三问的结果可知，10辆车的数量是不能把整个区域完全覆盖的，其算法与算法2类似，不同的是此时车的数目已经固定了，要求使D1,D2尽量大的满足，我们求得的评价指标值为，所得的巡逻方案见附件中的“1193402-Result5.txt〞所示。

        5.6            平均行驶速度提到时的巡逻方式和评价指标值

        问题六的分析方法与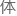实现与问题三一致，但是警车的接警后的平均速度由原来的提到，于是各分区的覆盖范围也增大了，将数值带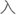问题3的算法中求解，      计算得的指标值为，其巡逻方案见附件中的“1193402-Result6.txt〞所示。

        图7            算法2框图

        六            模型的分析和评价

        在求解满足D1的条件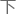，整个区域需要备多少辆警车问题中，采用分区巡逻的思想，先分析能使各区辖范围到达最大值时的规律，由特殊到一般层层行分析，逻辑严密，结果合理。

        在求解区域和警车数目时，在初步设定警车停靠位置的底上，用模拟退火算法思路构造函数来确定调整的概率大小，综合考虑了影响区间调整的因素后构造了函数来确定分区的调整方向，当分区照这两个调整函数行调整时，各分区能辖尽可能多的路节，所取得效果也比拟理想。